Elegant programming, part 2: object-oriented programming
Personal history
My first "serious"1 programming language was C, which I learned on the first, non-ANSI version of the hallowed Kernighan and Ritchie. Soon thereafter I began hearing about the elegance and power of object-oriented programming (OOP), so I picked up a book on C++, and began experimenting with it. It was a rough path! While C++ is now the standard language for many complex and high-performing systems and applications, it's probably not the best way to learn OOP. Indeed, after using C++ in my research for a few years, I attended a talk by the language's creator, Bjarne Stroustrup, entitled "Speaking C++ as a Native," and I realized that, well, I did not.
In Python, OOP follows a less strict, more pragmatic, and yet very powerful approach that does away with a lot of the boilerplate declarations and syntactic complexity required by C++. Moreover, Python's dynamic typing allows higher-order object magic (such as defining classes at runtime, or changing the class of an instance) that is just not possible with C++. In this chapter I won't try to teach you OOP theory, but I will give you a quick taste of working with objects in Python, using an example from quantitative biology (or maybe from screensaver theory). I bet you'll be left wanting more.
Before we get into it, let me tell you a few reasons why you should use OOP in your research. For sure, any program functionality that can be achieved with OOP can also be implemented with standard procedural programming. However:
- OOP eases your journey toward a working program;
- OOP helps you fight bugs and keep complications under control, by letting you think at a higher level;
- OOP allows you to easily reuse your code in future applications.
Like all powerful tools, OOP can be dangerous; for some tasks, it may just be overkill. Used correctly, it will make your scientific programming more joyful and productive, and that's the whole point of this book.
Wator
One of the most evocative Computational Recreations presented by A. K. Dewdney in the pages of Scientific American was Wator (Dewdney 1984), a simple simulation of a biological predator-prey model (itself a very interesting topic). Simulations simulator to Wator later appeared as screensavers in popular operating systems. Wator simulates the struggle for life between a predator species (the sharks) and its prey species (the fish). The animals behave very simply, moving randomly around, eating when they can, and spawning offspring periodically. The predators multiply when there is plenty of prey, but eventually they decimate their supply of food, and the predator population crashes by starvation; the prey then has a chance of rebuilding its numbers, and the cycle begins anew.
The rules of Wator
Wator takes place on a toroidal world covered by a thin ocean, which is represented by a rectangular grid with periodic boundary conditions.2 Each grid cell can be empty, or occupied by a fish or shark. The fish move around randomly; they eat ubiquitous and abundant plankton; and they reproduce every \(R_\mathrm{fish}\) time units. The sharks eat nearby fish if there any, and otherwise move around randomly; they reproduce every \(R_\mathrm{shark}\) time units; and they die of starvation if they haven't eaten for \(S_\mathrm{shark}\) time units. To keep things simple, reproduction is asexual, and old age is not a cause of death.
We're going to write our own Wator simulation. For this, the description of the simulation given above is not sufficient, and we need a set of detailed game rules that eliminates all ambiguities. Here it goes.
At the beginning of the simulation, the grid is initialized with the desired numbers of fish and sharks, which are placed randomly across the grid. All fish and sharks have individual gestation clocks, and all sharks have hunger clocks; these are all reset. At every time step, the fish move first. For every fish:
- The fish moves at random into one of the nearest-neighbor cells (i.e., north, south, east, or west) that are empty. If none is empty, the fish stays put.
- If the fish has moved and its gestation period has expired, a new fish is left in the previous location, and the gestation clocks of both fish are reset.
- The gestation clock of the fish is moved forward by one unit.
The sharks move second. For every shark:
- If there is a fish nearby, the shark eats it, and its hunger clock is reset.
- The shark moves at random into an empty nearest-neighbor cells. If none is empty, the shark stays put.
- If the shark has moved and its gestation period has expired, a new shark is left in the previous location, and the gestation clocks of both sharks are reset.
- If the shark's hunger period has expired, the shark dies and is removed from the grid.
- Otherwise, the gestation and hunger clocks are moved forward by one unit.
Choosing our objects
In OOP, objects are data structures combined with associated processing routines. They provide a way to organize code logically, and at a more fundamental level they provide a mechanism to abstract code functionality from the underlying implementation. This is a good idea for several reasons:
- it allows us to hide complex implementation details inside the objects, and to restrict the ways in which they can be used (abstraction/encapsulation);
- it allows us to use different objects as if they were the same (polymorphism);
- it allows us to build more complex objects from simple ones (composition and inheritance).
In most3 object-oriented languages, individual objects are instances of a class (much like individual animals are representatives of a species). The class defines properties and behaviors common to all instances. Each instance has its own identity; it is created and eventually destroyed; and it holds its own data values. The data elements of an object are known as attributes, while associated functions and procedures are known as methods (so we could call a method on an instance, and it would naturally use the instance's attributes).
But we should continue with our example.
Let us imagine a non-OOP implementation of Wator. We represent the grid as a two-dimensional array of integers, with every element encoding the content of a cell (say, with 0 for empty, 1 for fish, and 2 for shark). We also need a few more arrays to store the gestation and hunger clocks. At each time step, we then sweep through the grid array and apply the game rules. You may already some awkward aspects to this organization of the data: for instance, when we move the animals across the grid, we also have to move their clocks; furthermore, during each sweep we must distinguish the animals that have already moved from those that haven't, either by adding more cell codes, or by keeping separate arrays to represent the grid at the beginning and end of a time step. The logic of our code is getting complicated quickly; what is worse, we are forced to think about very nonessential issues. OOP to the rescue!
What will be our objects then? Certainly the animals, since they literally have behaviors, and they carry data (the clocks). So we will have a fish class and a shark class, with many instances corresponding to all the individual animals on the grid. The problem of evolving the state of each animal exactly once for each time step is solved easily by keeping the fish and sharks in two lists, and looping through these once per time step; fish and shark can have an evolve() method to... do their thing.
It is also a good idea to have an array-like grid object to keep track of the positions of the animals, and of who's whose neighbor. Otherwise, even if each animal held its own position (e.g., as a pair of Cartesian coordinates), in order to find its neighbors we would have to loop through all other animals, which seems too much trouble. Since Python does not have native arrays, grid can use a list of lists to hold the animals (or None if a cell is empty). At a minimum, grid should have an initialization method to populate it with animals. If grid holds also the lists of all fish and sharks, we can give it its own evolve() method to take all the animals through one time step. (By the way, it's not a problem for the same object to be in two lists at once, since Python lists hold references to objects – if you know C, think pointers – rather than the actual things.)
Let us recap what we have so far:
| class | attributes | methods |
|---|---|---|
fish and shark |
gestation/hunger clocks; grid position | evolve() |
grid |
a list of lists, holding references to the animals; a list of all fish; a list of all sharks | initialization; evolve() |
This could work, but I'm not too happy yet with the handling of grid positions as Cartesian coordinates. It violates encapsulation, because it requires fish and shark to know about the internal grid representation, and to worry about such details as periodic boundary conditions. We can improve this arrangement by filling the grid with smart cell objects that know which animal they contain (if any), and which other cells are their neighbors. Instead of Cartesian coordinates, the animals can hold a reference to their cell, and request the list of its neighbors.
Thus we revise our OOP plan:
| class | attributes | methods |
|---|---|---|
fish and shark |
gestation/hunger clocks, cell reference | evolve() |
cell |
reference to animal (or None); list of neighboring cells |
place(animal), to establish a birectional link between cell and animal |
grid |
a list of lists of cells; a list of all fish; a list of all sharks |
evolve() |
A Python Wator
We're ready to write some code! This may be a good time to (re-)familiarize yourself with the Python class mechanism. Remember that:
Classes are defined with the
classkeyword, followed by an indented block that includes all method definitions. For instance,
You may consider the appearance ofclass fish(object): def evolve(self): [...] [...]objectsimply as a Python idiom. Sincefishdoes not have any other parent class of our making, we indicate explicitly that it inherits from the basic Python classobject. We'll talk about inheritance later.- Attributes and methods are accessed using the dot operator on the instance (e.g.,
a_fish.gclock,a_fish.evolve()). - Method definitions always include as their first argument a reference (usually named
self) to the instance on which the method is called (soa_fish.evolve()would automatically setselftoa_fishwithin the body of the method). - Instances are created by calling the class name as a function (e.g.,
a_fish = fish(...)), which sets up the object and invokes the initialization method__init__(self,...). - Attributes don't need to be declared explicitly; they are created by assignment (e.g.,
a_fish.gclock = 0, orself.gclock = 0inside a method). An attribute can also be assigned to the class, and its value is then shared by all instances (e.g.,fish.gperiod = 3, or simplygperiod = 3inside the class definition). There are several other features in the Python class implementation (some of them subtle, most of them very useful), but we won't need them here.
Here's our first, yet incomplete, attempt at wator.py:
# file wator.py
import random
class fish(object):
# define a _class attribute_ shared among all fish
gperiod = 3
def __init__(self):
# define an individual _instance attribute_
self.gclock = 0
class shark(object):
gperiod = 10
speriod = 3
def __init__(self):
self.gclock = 0
self.sclock = 0
class cell(object):
def __init__(self):
# cells will be empty by default
self.content = None
# establish a bidirectional reference between cell and animal
def place(self,animal):
self.content = animal
animal.cell = self
class grid(object):
# initialize an MxM grid with N_fish and N_shark animals of the two species
def __init__(self,M,N_fish,N_shark):
# make a list of lists, where each element is a new `cell`;
# thus cells can be accessed as self.cells[i][j]
self.cells = [[cell() for j in range(M)] for i in range(M)]
# create the list of nearest neighbors for each cell
for i in range(M):
for j in range(M):
# periodic boundaries are handled by the modulo operator `%`
# check: for i,j = 0 to M-1, we have M % M = 0, -1 % M = M-1
self.cells[i][j].neighbors = (self.cells[i][(j+1) % M],
self.cells[i][(j-1) % M],
self.cells[(i+1) % M][j],
self.cells[(i-1) % M][j])
# create all fish and shark individuals
self.allfish = [fish() for i in range(N_fish)]
self.allsharks = [shark() for i in range(N_shark)]
# to place the fish and sharks on the grid, we have to make sure that
# we don't use the same cell twice, so we keep a (flat) list of empty cells
empty = [gridcell for row in self.cells for gridcell in row]
# loop over all animals (notice the lovely notation to concatenate lists)
for animal in self.allfish + self.allsharks:
# remove a cell at a random position from the `empty` list
randomcell = empty.pop(random.randrange(len(empty)))
# place the animal there
randomcell.place(animal)
This is all very clean and pleasant: we have used Python list comprehensions to good effect. Moreover, the code flows clearly from the conceptual definition of the objects that we worked out above. The only place where I had to think twice was the initial placement of the animals. A simpler (but, in my opinion, uglier) solution might have been to keep trying random positions for each animal until an empty cell is found:
# (no need to make the `empty` list)
for animal in self.allfish + self.allsharks:
while True:
randomcell = self.cells[random.randrange(M)][random.randrange(M)]
if randomcell.content is None: # if we found an empty cell:
randomcell.place(animal) # place the animal
break # break the infinite loop
Now we can then try our hand at the fish.evolve() method.
class fish(object):
[...]
def evolve(self):
# find empty neighbors...
empty = [neighbor for neighbor in self.cell.neighbors if neighbor.content is None]
# if there is at least one, we can move there, and perhaps spawn
if empty:
if self.gclock >= self.gperiod: # if the gestation clock is past due:
self.cell.place(fish()) # place a new fish at the current position
self.gclock = 0 # reset the gestation clock
else:
self.cell.content = None # otherwise, empty the current location
# choose an empty neighbor at random and move there
dest = random.choice(empty)
dest.place(self)
self.gclock = self.gclock + 1
Note to ourselves: when we make a new fish inside a_fish.evolve() we place it inside the right cell, but we have no way of adding it to the global list allfish (which belongs to a grid instance), so we must remember to make that list anew at the end of every grid.evolve() call. (But if we wanted to update the list immediately, we could hold a reference to the grid instance in each cell instance.)
The shark.evolve() method comes next. We could just copy fish.evolve() and add code to handle the business of eating and starving. But duplicating code is never a good idea—if later we revise the mechanics of spawning, we will have to change it in two places. Moreover, I want to teach you about inheritance in OOP, so we'll make shark a subclass of fish (the base class), which lets shark inherit all the fish methods. After all, sharks are fish! The subclass can add its own methods and it can override the methods of the same name defined in the base class (but even then, it can still access those with super()). In the context of Wator, we will write a new shark.evolve() that takes care of eating, and that will call fish.evolve() to handle the spawning and moving.
class shark(fish):
[...]
def evolve(self):
# find food nearby [see note 1 below]
food = [neighbor for neighbor in self.cell.neighbors if type(neighbor.content) is fish]
if food: # if there is any:
prey = random.choice(food) # choose one at random
prey.content = None # remove it from the grid [2]
self.sclock = 0 # reset the starvation clock
# now move and spawn using fish.evolve() [3]
super(shark,self).evolve()
if self.sclock >= self.speriod: # if the starvation clock is expired
self.cell.content = None # die by removing ourselves from the grid [2]
else:
self.sclock = self.sclock + 1
Three notes:
- In Python,
type(A)returns the exact class of the instanceA. A more general formulation of the test isisinstance(A,B), which isTruealso whenAis an instance of a subclass ofB; but that's not appropriate in this case becausesharks arefish, and we do not wish them to eat other sharks. - Animal death is handled by removing the reference to the animal in its old cell. This ensures that the animal won't be evolved at the next time step, because by then we will have built new
allfishandallsharksfrom the grid. Furthermore, once the lists are rebuilt there remains no reference to the dead animal in any of our data structures, so Python will destroy the corresponding instance. This is a very convenient way to handle memory deallocation without giving it much thought.4 - I'm sorry that I have to introduce this construct, which is not the prettiest,5 at this early time: in Python
super(class,instance)returns a "view" of a subclass instance as an instance of the parent class. So when we callevolve()onsuper(shark,self)we getfish.evolve()rather thanshark.evolve().
Great! We must still change the fish.evolve() method slightly, so that it will spawn a new shark, rather than a fish, when it's called from shark. This sounds harder than it is: instances are created by calling the class name as a function, and we get the class of an instance with type(self). Furthermore, fish.evolve() uses self.gperiod, which will be automatically set to shark.gperiod for a shark instance. No change is needed there.
class fish(object):
[...]
def evolve(self):
empty = [neighbor for neighbor in self.cell.neighbors if neighbor.content is None]
if empty:
if self.gclock >= self.gperiod:
self.cell.place(type(self)()) # make an animal of the right kind
self.gclock = 0
dest = random.choice(empty)
dest.place(self)
self.gclock = self.gclock + 1
Finally we can write grid.evolve(), which will just call evolve() on all the animals in its list, and then update the lists from the grid.
class grid(object):
[...]
def evolve(self):
for animal in self.allfish + self.allsharks:
animal.evolve()
# collect all fish and sharks from the grid
self.allfish = [gridcell.content for row in self.cells
for gridcell in row if type(gridcell.content) is fish]
self.allsharks = [gridcell.content for row in self.cells
for gridcell in row if type(gridcell.content) is shark]
# as a bonus, return up-to-date population numbers
return len(self.allfish), len(self.allsharks)
We also need a "main" function to initialize the grid and call grid.evolve() repeatedly. We'll be minimalistic for the moment, and take just two arguments, for the linear size of the grid and for the number of steps to run:
import sys, numpy as N, matplotlib.pyplot as P
M, steps = int(sys.argv[1]), int(sys.argv[2])
# populate 20% of the grid with fish, 5% with sharks
mygrid = grid(M=50,N_fish=int(0.2*M**2),N_shark=int(0.05*M**2))
# evolve repeatedly, collecting population numbers
populations = N.zeros((steps,2))
for step in range(steps):
populations[step,:] = mygrid.evolve()
# make a simple plot
P.plot(populations[:,0]); P.hold(True)
P.plot(populations[:,1]); P.hold(False)
P.show()
It works! We observe the expected cyclical fluctuations in the number of animals. The sharks also exhibit a shorter-period fluctuation that seems related to their starvation clocks.
>>> python wator.py 50 400
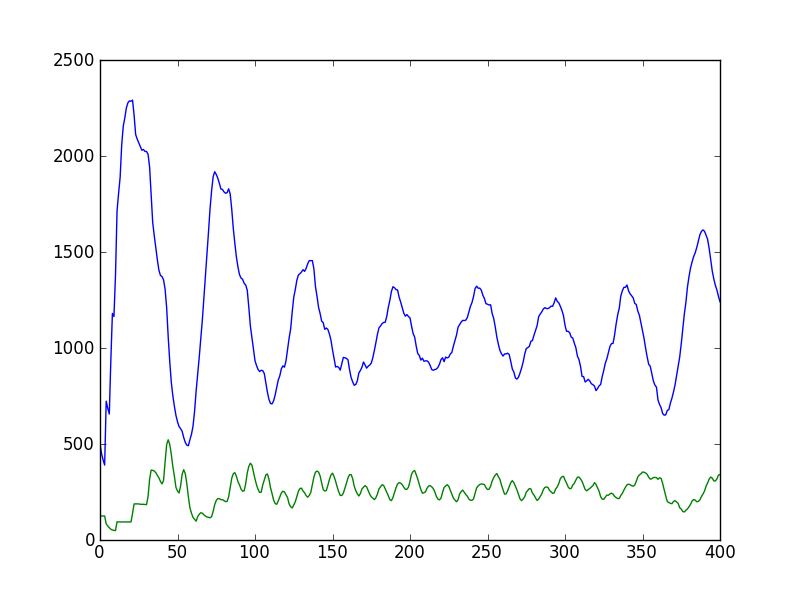
400 steps on a 50x50 Wator grid, as simulated by wator.py. The blue (green) line plots the number of fish (sharks).
Final comments
Let us take a minute to look at our code again, copied here in its entirety. I have muted the comments somewhat, especially where the Python constructs and our naming choices already convey the logic of the program. I have also added Python docstrings to document the only functions meant for the "public" (the grid constructor and grid.evolve()).
import random
class fish(object):
gperiod = 3
def __init__(self):
self.gclock = 0
def evolve(self):
empty = [neighbor for neighbor in self.cell.neighbors if neighbor.content is None]
if empty: # if there's an empty cell nearby:
if self.gclock >= self.gperiod: # if the gestation clock is past due:
self.cell.place(type(self)()) # place a new animal at the current position
self.gclock = 0 # reset the gestation clock
else:
self.cell.content = None # otherwise, empty the current location
dest = random.choice(empty) # choose random empty neighbor and move there
dest.place(self)
self.gclock = self.gclock + 1
class shark(fish):
gperiod = 10
speriod = 3
def __init__(self):
self.gclock = 0
self.sclock = 0
def evolve(self):
food = [neighbor for neighbor in self.cell.neighbors if type(neighbor.content) is fish]
if food: # if there is fish nearby:
prey = random.choice(food) # choose a fish at random
prey.content = None # remove it from the grid
self.sclock = 0 # reset the starvation clock
super(shark,self).evolve() # move and spawn using fish.evolve()
if self.sclock >= self.speriod: # if the starvation clock is expired
self.cell.content = None # die and remove ourselves from the grid
else:
self.sclock = self.sclock + 1
class cell(object):
def __init__(self,grid):
self.content = None
def place(self,animal):
self.content = animal
animal.cell = self
class grid(object):
def __init__(self,M,N_fish,N_shark):
"""Create an MxM Wator grid and populate it wth N_fish fish and N_shark sharks."""
self.cells = [[cell(self) for j in range(M)] for i in range(M)]
for i in range(M):
for j in range(M):
# square-grid neighbors, periodic boundary conditions
self.cells[i][j].neighbors = (self.cells[i][(j+1) % M],
self.cells[i][(j-1) % M],
self.cells[(i+1) % M][j],
self.cells[(i-1) % M][j])
self.allfish = [fish() for i in range(N_fish)]
self.allsharks = [shark() for i in range(N_shark)]
# keep a flattened list of empty cells
empty = [gridcell for row in self.cells for gridcell in row]
for animal in self.allfish + self.allsharks:
# remove a random cell from `empty`, place animal there
randomcell = empty.pop(random.randrange(len(empty)))
randomcell.place(animal)
def evolve(self):
"""Evolve the Wator grid through one time step, return the tuple (N_fish,N_shark)."""
for animal in self.allfish + self.allsharks:
animal.evolve()
# gather all the fish and sharks from the grid
self.allfish = [gridcell.content for row in self.cells
for gridcell in row if type(gridcell.content) is fish]
self.allsharks = [gridcell.content for row in self.cells
for gridcell in row if type(gridcell.content) is shark]
return len(self.allfish), len(self.allsharks)
import sys, numpy as N, matplotlib.pyplot as P
M, steps = int(sys.argv[1]), int(sys.argv[2])
mygrid = grid(M=50,N_fish=int(0.2*M**2),N_shark=int(0.05*M**2))
populations = N.zeros((steps,2))
for step in range(steps):
populations[step,:] = mygrid.evolve()
P.plot(populations[:,0]); P.hold(True)
P.plot(populations[:,1]); P.hold(False)
P.show()
All in all, it took us a little more than 100 lines of code, including comments and generous spacing, to write a functional Wator simulation. The code is rather readable, and different aspects of the rules of the game are nicely embodied by different objects, in a nice demonstration of the OOP principle of abstraction/encapsulation. The fact that we can call evolve() (or evaluate gperiod) on any animal instance and that Python will then use the appropriate implementation (or value) defined in fish or shark demonstrates the OOP principle of polymorphism: fish and shark are different forms of the same underlying object.
In this case, we obtained the polymorphic behavior using Python's class inheritance mechanism, by defining shark as a subclass of fish. However, even if we had defined the shark class independently, by duplicating the spawning/moving code as needed, we could still have exploited polymorphism by calling evolve() on an animal object without knowing its type a priori. This is because Python allows (encourages!) polymorphism by dynamic (or duck) typing:
When I see a bird that walks like a duck and swims like a duck and quacks like a duck, I call that bird a duck.6 (Attributed to James Whitcomb Riley.)
That is, it is the methods and properties defined for an instance that determine how it can be used, rather than its actual class or inheritance. Duck typing is perhaps the main reason why OOP feels so casual and friendly in Python (as opposed to, say, C++). Beyond the official Python guide, there are many good books (Lutz 2009, Phillips 2010) and web tutorials (Gauld, Lott) where you can learn a lot more. We'll also come back to Python OOP in Chapter XX, where we will use some higher-order magic to build a generic framework for Markov-Chain Monte Carlo integration.
Problems
Exercise 1 – Fun with Wator
Play with the program, and watch how population dynamics changes when you change \(R_\mathrm{fish}\), \(R_\mathrm{shark}\), \(S_\mathrm{shark}\), and the grid size. Instead of plotting time series \(N_\mathrm{fish}(t)\) and \(N_\mathrm{shark}(t)\), generate a phase-space plot (\(N_\mathrm{fish}\) vs. \(N_\mathrm{shark}\)). Using matplotlib's imshow, create and animation of the evolving grid.
Exercise 2 - More Wators
Our abstract implementation of the nearest-neighbor relation allows us to explore variants with little effort. Change the assignment of cell.neighbors in grid.__init__() to implement a hexagonal grid. (Even better, move out the definition of nearest neighbors in a separate method, and redefine it in a hexgrid subclass of grid.) Now every animal has six nearest neighbors: how does this affect the dynamics of the game?
Exercise 3 – Differential Wator
Work out the continuous Lotka–Volterra equations that correspond to an idealized version of Wator. You will have to think about the probability of spawning, starving, eating, and being eaten for an "average" fish or shark. Using scipy's odeint, integrate the equations numerically and plot the resulting curves.
References
Dewdney, A. K. 1984. “Computer Recreations: Sharks and fish wage an ecological war on the toroidal planet Wa-Tor.” Scientific American 251: 14-22.
Although it probably takes place on a periodic grid explained as a toroidal world. ↩
Prototype-based languages have instances, but not classes. ↩
In Python implementations other than CPython, the object may not be destroyed instantly when it is no longer reachable. ↩
Python 3 allows the nicer
super(), without arguments, to achieve the same effect. ↩I know, we're mixing up our animals here... ↩