Michele's research
Nonlinear evolution of r-modes in young, hot neutron stars
Synopsis
All rotating stars possess a class of circulation modes (r-modes) that are driven toward instability by gravitational radiation reaction. In the hot, rapidly rotating neutron stars that come fresh out of a supernova explosion, this destabilizing force is strong enough to dominate the internal viscous dissipation of the star. So it is expected that the amplitude of the r-mode will grow enormously within ten minutes of the birth of the star. The growth of the r-mode converts rotational energy into mode energy, while gravitational radiation removes angular momentum from the star. Eventually the r-mode should saturate, although no one really knows by what process.
The strength of the radiation emitted and the amount of the angular momentum removed depend critically on the maximum mode amplitude. In collaboration with Lee Lindblom and Joel E. Tohline, I investigated the growth of the r-modes by solving numerically the nonlinear hydrodynamic equations that describe their evolution. In our simulations, the circulation velocities of the mode grow to be comparable to the rotation velocity of the star; then strong shocks develop which damp the mode quickly. Before they do so, the star loses about 40 percent of its initial angular momentum. The nonlinear evolution creates a strong differential rotation, which is concentrated near the surface and especially near the poles of the star.
-
Non-linear evolution of the r-modes in neutron stars
L. Lindblom, J. Tohline, and M. Vallisneri
Phys. Rev. Lett. 86, 1152 (2001) [+] -
Numerical evolutions of nonlinear r-modes in neutron stars
L. Lindblom, J. Tohline, and M. Vallisneri
Phys. Rev. D 65, 084039 (2002) [+] - Old rmode project page at CACR.
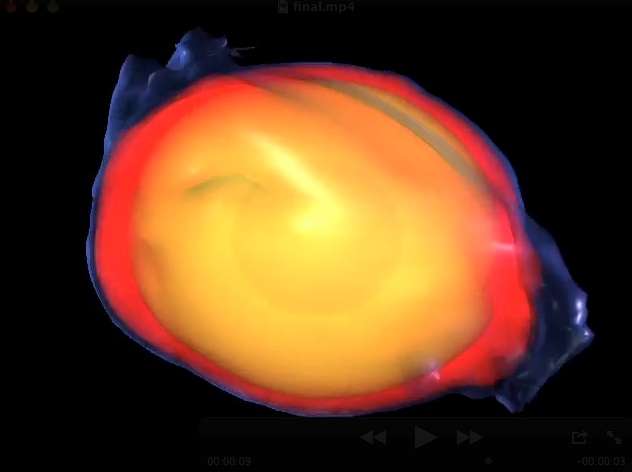
r-mode, the movie
The numerical code used in our simulation solves the Newtonian equations of hydrodynamics in a rotating reference frame, using the Fortran 90 code developed at LSU by Joel Tohline to study a variety of astrophysical problems.
This movie shows the final stages of the nonlinear evolution of the stellar model. Even if the r-mode is primarily a circulation mode, at high amplitudes a correlated perturbation appears also in the density. The density perturbation grows and finally creates cresting waves on the surfaces. The strong shocks associated with the cresting waves dissipate enough energy to damp the r-modes, and destroy the density perturbation pattern.
In the press
- Research brief on Progress on the nonlinear r-mode problem [Keith Lockitch, Matters of Gravity 17 (2001)]
- "News and views" item in Nature on this research [Chris Fryer and Stan Woosley, Nature 411, 31 (2001)]
- Cover feature on this research in enVision, the NPACI and SDSC quarterly science magazine [Paul Tooby, enVision 17, vol. 2 (2001); see also the front cover]
- News item on this research on the CACR website [Sarah Emery Bunn, Caltech Center for Advanced Computing Research (July 2001)]
- News item on this research on the LIGO web newsletter [Gregory Mendell, LIGO (April 2001)]
Back to research gallery.
© M. Vallisneri 2014 — last modified on 2012/05/15