Michele's research
GW detection by pulsar timing
At very low frequencies (1/year), the accurate timing of multiple intrinsically stable pulsars in the Galaxy can be used to search for GWs from supermassive–black-hole binaries or cosmic-string networks. The GW sources imprint the times of arrival of the pulses with characteristic delays and advances, at a level (10-100 ns) comparable to the timing stability of the best millisecond pulsars. Thus, an array of such systems (a pulsar-timing array, or PTA) constitutes a powerful GW detector.
I am a member of the north-American PTA collaboration, NANOGrav. My group currently includes JPL/Caltech astronomers Joseph Lazio, Walid Majid, and Curt Cutler, Einstein fellows Rutger van Haasteren and Justin Ellis, NASA postdoc Stephen Taylor, and Marie Curie fellow Chiara Mingarelli. The focus of our group is on the application of Bayesian-inference methods to data analysis problems in pulsar timing, including the intrinsic-noise characterization of pulsars, the statistical analysis of timing models beyond the usual linear least-square fits, and more.
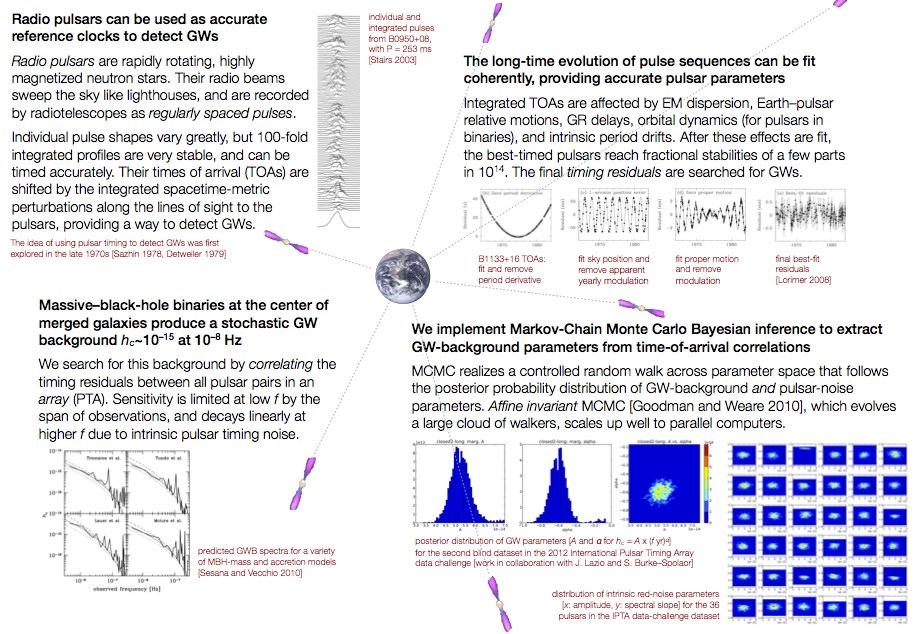
An overview of pulsar-timing GW detection (from JPL RTD poster fair, Nov 2012). PDF.
New advances in the Gaussian-process approach to pulsar-timing data analysis
Gaussian processes are the generalization of random variables to functions. They are extremely useful to represent time-correlated stochastic signals and other sources of uncertainties distinct from measurement errors (such as unmodeled physics). In this work we review, refine, and extend the application of Gaussian processes to modeling noise in pulsar-timing data analysis. Such a description was implicit in earlier formulations of statistical inference for pulsar timing, and here we make it fully explicit, gaining access to the wealth of results about Gaussian processes in the machine-learning literature.
We also derive insightful and/or optimized representations for the likelihood expressions that are needed in Bayesian inference on pulsar-timing-array datasets. In Bayesian inference, we need to sample the likelihood at many locations in parameter space, which is usually achieved with a Markov Chain Monte Carlo (or closely related) sampling scheme. Armed with our likelihood representations, we obtain two improved parameter-sampling schemes inspired by Gibbs sampling. The new schemes have vastly lower chain autocorrelation lengths than current state-of-the-art methods, potentially speeding up Bayesian inference by orders of magnitude. The new samplers can be used for a full-noise-model analysis of the large datasets assembled by the International Pulsar Timing Array collaboration, which present a serious computational challenge to existing methods.
-
New advances in the Gaussian-process approach to pulsar-timing data analysis
R. van Haasteren and M. Vallisneri
Phys. Rev. D 90, 104012 (2014) [+]

Correlation profile for the amplitude and spectral-slope parameters of timing noise, as sampled in a Markov-Chain Monte Carlo run. The white level curves show the range of an individual Markov-chain update of the parameters.
Low-rank approximations for large stationary covariance matrices
Many data-analysis problems involve large dense matrices that describe the covariance of stationary noise processes; the computational cost of inverting these matrices, or equivalently of solving linear systems that contain them, is often a practical limit for the analysis. In this paper we describe two general, practical, and accurate methods to approximate stationary covariance matrices as low-rank matrix products featuring carefully chosen spectral components. These methods can be used to greatly accelerate data-analysis methods in the Bayesian and generalized-least-squares analysis of pulsar-timing residuals, and in many other contexts in machine learning and other disciplines.
-
Low-rank approximations for large stationary covariance matrices, as used in the Bayesian and generalized-least-squares analysis of pulsar-timing data
R. van Haasteren and M. Vallisneri
MNRAS 446, 1170 (2015) [+]
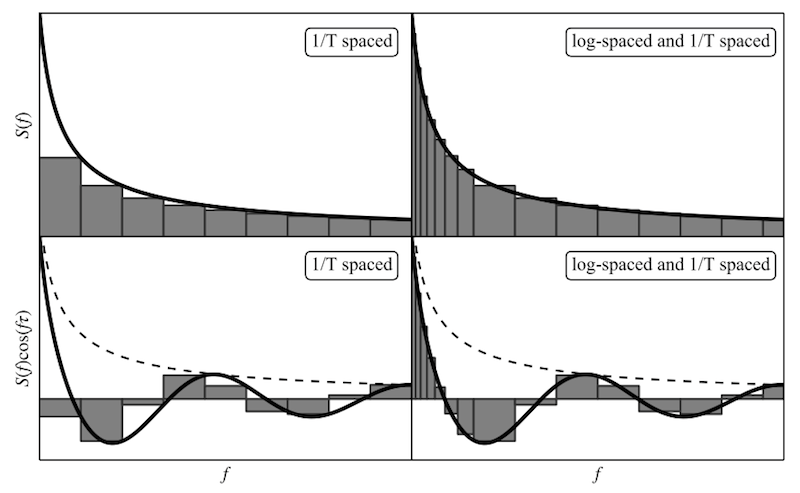
Approximating the Wiener—Khinchin integral (which maps the power spectral density S(f) to the covariance C(t)) with regularly spaced frequency components, and with logarithmically spaced components, as prescribed in one of our improved approximation methods.
Bayesian inference for pulsar timing models
Because of their extremely regular periodic emission, millisecond pulsars are incredible laboratories not just for detecting gravitational waves, but also for studying neutron-star astrophysics and general relativity. These studies require fitting the observed pulse time of arrivals to complicated timing models, which describe numerous effects such as the astrometry of the source, the evolution of the pulsar's spin, the presence of a binary companion, and the propagation of the pulses through the interstellar medium. The fits are usually performed with a simple least-squares techniques that linearizes the model with respect to all the fit parameters. Sarah Vigeland and I experimented instead with using full nonlinear Bayesian inference for this purpose. The benefits of doing so include:
- validating least-squares fits when these are correct, and characterizing parameter uncertainties properly when they are not;
- incorporating prior parameter information (for instance, dispersion-measure distances from electron density maps, or VLBI position determinations);
- dealing with noise models with a priori unknown parameters;
- and even comparing alternative models (for instance, a pure-general-relativity description of binary orbits with a modified-gravity solution).
Our computational setup combines the standard timing models of tempo2 with the nested-sampling integrator MultiNest. In our paper, we focus on three NANOGrav pulsars (B1953+29, J2317+1439, and J1640+2224), which demonstrate a variety of benefits from Bayesian analysis.
-
Bayesian inference for pulsar timing models
S. J. Vigeland and M. Vallisneri
MNRAS 440, 1446 (2014) [+]
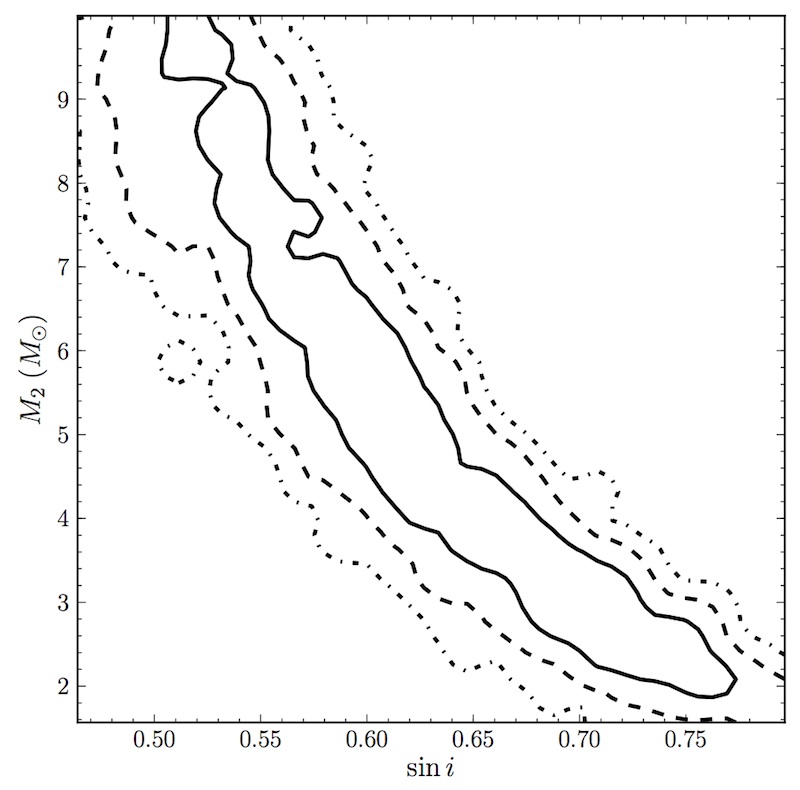
Joint posterior distribution for the inclination and companion-mass parameters for PSR J1640+2224. This distribution is intringuingly different from the previously established description of this system.
Characterizing the gravitational-wave discovery space of pulsar timing arrays
So far, the implementation of GW searches using PTAs has focused mainly on three source types, considered especially promising: supermassive–black-hole binaries, cosmic strings, and the stochastic background from early-Universe phase transitions. By contrast, our JPL group examined the potential of PTAs for discovering unanticipated sources, and derived detection constraints based only on simple energetic and statistical considerations (in the spirit of the famous, but not widely read, "cherished beliefs" paper by Zimmermann and Thorne).
We showed that a PTA detection of GWs at frequencies above 3 10–5 Hz would either be an extraordinary coincidence or violate our cherished beliefs. We showed also that GW memory can be more detectable than direct GWs, and that, as we consider events at higher and higher redshifts, the memory effect increasingly dominates an event's total signal-to-noise ratio. The paper includes also a simple analysis of the effects of a pulsar's intrinsic red noise in PTA searches, and a demonstration that the periodic GWs in the 10–8–10–4.5 Hz band would not be absorbed by fitting pulsar parameters (which is always done).
-
The gravitational-wave discovery space of pulsar timing arrays
C. Cutler, S. Burke-Spolaor, M. Vallisneri, J. Lazio, and W. Majid
PRD 89, 042003 (2014) [+]
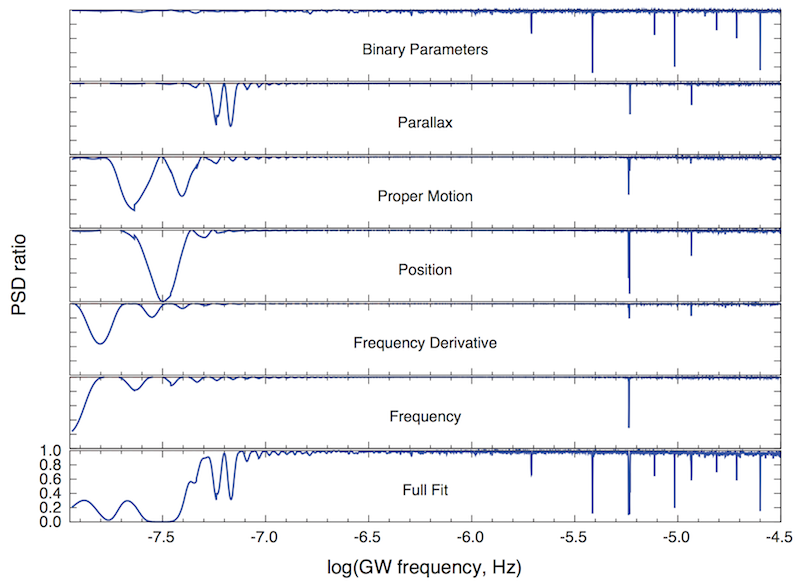
Gravitational-wave power absorbed by fitting for various timing parameters, for pulsar J0613-0200. This simulation demonstrates that high-frequency GWs at most frequencies would survive through timing-model fits. (Plot by Sarah Burke–Spolaor.)
The International Pulsar Timing Array mock data challenge
The International Pulsar Timing Array (IPTA) is a consortium comprising the European PTA, NANOGrav, and the Australian Parkes PTA. The goal of the IPTA is to detect GWs using an array of the 30 “best” pulsars, timed with various radiotelescopes. In March 2012, it released its first mock data challenge, with the purpose of introducing researchers to the formats and peculiarities of pulsar-timing data; of helping agreement in defining parameters and the significance of measurements; and of providing the first blind test of GW data-analysis pipelines. For this challenge, I developed a Bayesian-inference code to search for a GW stochastic background from supermassive–black-hole binaries.
- See our entry to the IPTA mock data challenge.
- Visit the GitHub repository for our search pipeline.
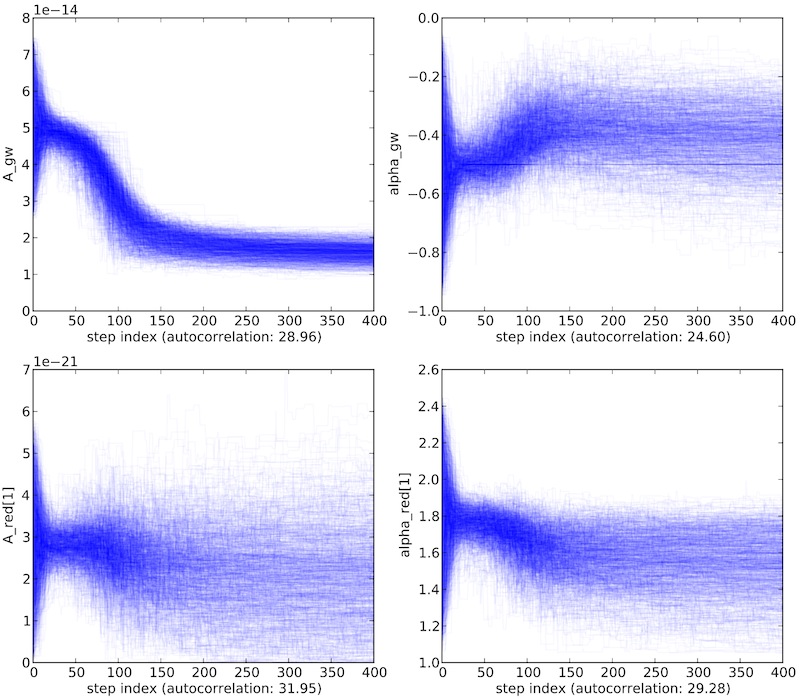
Convergence of Monte Carlo chains in one of our IPTA mock-data-challenge entries.
Back to research gallery.
© M. Vallisneri 2014 — last modified on 2014/10/28