vallis.org

Michele's research

Statistical and computational methods for GW data analysis

Detecting modified gravity and the "fundamental bias"

We use gravitational waveforms computed in general relativity to search for GW sources such as inspiraling binaries of compact objects, and we will use them to estimate source parameters once we have confirmed detections. However, if the strong-field regime of the gravitational interaction were to deviate from the predictions of GR, our parameter estimation may be affected by a systematic fundamental bias due to using incorrect waveforms. In this paper Nico Yunes and I develop a scheme (based on my prior work in PRD 76 and PRD 86, discussed below) to determine in which cases the deviations from GR are not large enough to be detectable on their own, and yet the systematic parameter-estimation errors remain significant—larger than the statistical uncertainties due to detector noise.

For a given observation, the answer depends on the strength of the signal and the magnitude of the modified-gravity correction. As an example, we study three representative stellar-mass binary systems that will be detectable with second-generation ground-based observatories such as Advanced LIGO. We find that significant systematic biases can occur whether or not modified gravity can be positively detected, for correction magnitudes that are not currently excluded by any other experiment.

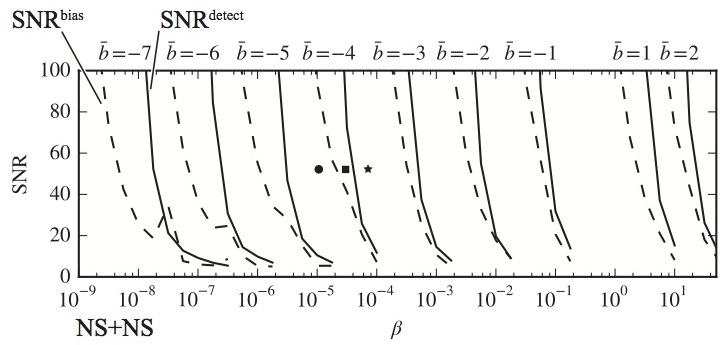
For different modified-gravity phasing-correction exponents b and strengths β, this figure compares the detection SNRbias at which the fundamental bias becomes larger than the statistical error with the SNRdetect at which modified gravity can be detected by way of Bayesian model comparison. Unrecognized fundamental biases occur in the region between the solid and dashed curves.

A general formalism to characterize the reach of tests of general relativity with gravitational waves

Gravitational waves from binary inspirals and other sources can be used to test general relativity for self consistency, and against alternative theories of gravity. For most tests, and for sufficiently strong signals, I show that there is a simple way to see how well we can do: the SNR1 required for alternative-gravity detection is a simple function of the fitting factor2 between general-relativity and alternative-gravity waveforms (i.e., the extent to which the former can be made to resemble the latter by altering their physical parameters).

For instance, second-generation ground-based detectors such as Advanced LIGO would detect alternative-gravity corrections to standard general-relativistic waveforms if the corrections are no smaller than 1–10%, corresponding to fitting factors of 0.9–0.99. Thus, it is only with the much higher-SNR detections of future space-based detectors that we will be able to perform accurate tests of general relativity.

1The signal-to-noise ratio—the strength of the signal relative to the detector noise.
2The extent to which the former can be made to resemble the latter by altering their physical parameters.

Poster on my formalism, presented at the KITP "Rattle and Shine" workshop on GW and EM studies of compact binary mergers (Jul 30–Aug 3, 2012). PDF.

Mapping the distribution of the maximum-likelihood estimator

In gravitational-wave astronomy, we often wish to characterize how well we will be able to extract physical source parameters from a detection. There are two ways to do so: a frequentist statistician would derive a single best parameter estimate (the maximum-likelihood estimator) from the observation, and then study how much it moves around in parameter space because of noise, in a hypothetical infinite series of observations featuring the same source, but different noise; a Bayesian statistician would derive the posterior probability distribution for the source parameters in the observation we have.

If the signal is sufficiently strong, the (in)famous, easily computed Fisher information matrix (see below) provides an accurate mathematical description of both cases. However, signals will seldom be strong enough, at least in initial observations. In this paper I provide an alternative, exact method to map the distribution of the maximum-likelihood estimator for signals of any strength. This technique can help the frequentist as well as the Bayesian, and it can be applied to inference problems well beyond the walls of gravitational-wave astronomy.

  • Beyond the Fisher-matrix formalism: exact sampling distributions of the maximum-likelihood estimator in gravitational-wave parameter estimation
    M. Vallisneri
    Phys. Rev. Lett. 107, 191104 (2011) [+]

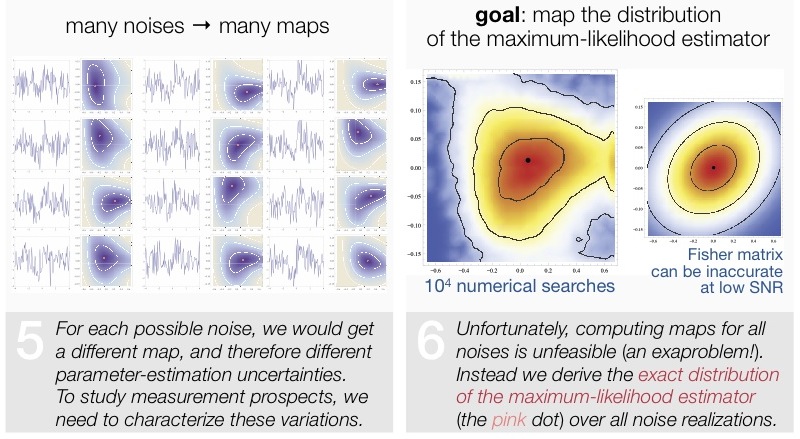
A graphical explanation of this method (from JPL RTD poster fair, Nov 2011). PDF (8 Mb).

The Fisher information matrix

The Fisher matrix is an easily computed mathematical object that is widely used to predict the parameter-estimation performance of gravitational-wave observations from the local dependence of the waveforms on the source parameters. Unfortunately, Fisher-matrix analyses can often be incorrect, especially for complicated waveforms or relatively weak signals; until now there have been no straightforward criteria to decide when this is the case.

In this work I provide practical tools to diagnose the correctness of the Fisher-matrix formalism for specific observations. In particular, I discuss what happens when some source parameters influence waveforms only weakly; when it is necessary to take into account the prior probabilities of source parameters; and, most important, when gravitational-wave signals can be considered strong enough to believe Fisher-matrix results. I also extend the formalism to include terms of higher order in the local dependence of the waveforms on the source parameters.

  • Use and Abuse of the Fisher Information Matrix in the Assessment of Gravitational-Wave Parameter-Estimation Prospects
    M. Vallisneri
    Phys. Rev. D 77, 042001 (2008) [+]

Systematic error from imperfect signal templates

When we talk about the expected accuracy for gravitational-wave observations we usually refer to the errors induced by instrument noise (say, as predicted by the Fisher matrix), but there is often an unspoken assumption that the theoretical errors due to inaccuracies in our models of the waveforms are negligible by comparison. However, the mergers of supermassive–black-hole binaries will appear in the LISA data with such contrast over noise that we wonder whether our waveform models are truly accurate enough.

In this work with Curt Cutler, we develop a computationally efficient method to estimate these theoretical errors, and we apply it to the LISA observations of supermassive–black-hole binaries. Using a somewhat simplified model of these waveforms, we conclude that for the strongest signals the theoretical errors will be larger than the noise-induced errors, and therefore additional modeling work may be needed to draw the maximum scientific payoff from the LISA observations. However, the expected theoretical errors in the determination of sky position (a crucial piece of information that will be used for optical searches of electromagnetic counterparts to the mergers) appear to be already under control.

  • LISA detections of massive black hole inspirals: parameter extraction errors due to inaccurate template waveforms
    C. Cutler and M. Vallisneri
    Phys. Rev. D 76, 104018 (2007) [+]

Back to research gallery.

© M. Vallisneri 2014 — last modified on 2013/11/05

Tantum in modicis, quantum in maximis